Best overlap between curves

Introduction

Given two curves $y1(x)$ and $y2(x)$ how can we find the best overlap of those two curves ?

The notion of "best overlap" refers to the minimisation of a distance between the curves. Definin the distance is thus the first step.

In the following examples, we will take the distance between two curves as the quadratic difference.

Provided that $y1$ and $y2$ have the same number of points $N$, we define the distance as follows:

$$d(y1, y2) = \sum_{i=0}^{N-1} \left[y_1(x_i) - y_2(x_i) \right]^2 $$

Now, we supposed that the the curves are considered at the same locations $x_i$, so we will just use the index $i$ to tag the values of y in a array of length $N$:

$$d(y1, y2) = \sum_{i=0}^{N-1} \left(y_{1,i} - y_{2,i} \right)^2 $$

Intuitively, finding the best overlap would just consist in making a curve "glide" horizontally while keeping the other fixed. Then, for each increment of translation, we would compute the distance and try to get the minimum among all the computed distances. This would give us the "best" overlap.

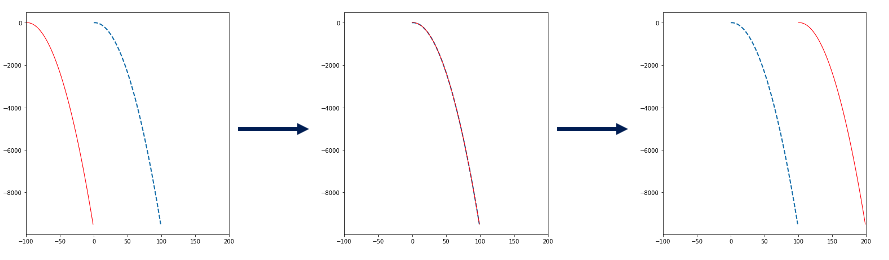
Here I would like to mention two things:

1. We may be tempted to go for a convolution product because it seems to be exactly what we are trying to do. However, as I will show later it doesn't work.

2. The problem that will come quickly is how to compare the distance between two sets of curves, where both sets are of different lengths (number of points). We need to renormalize it, otherwise, a bad overlap between two short pieces may yield a better distance than a good yet non perfect overlap between two long pieces of curve.

We will call $d_{m}$ the normalized distance and define it as follows:

$$d_{m}(y1, y2) = \frac{d(y1,y2)}{N} = \frac{1}{N} \sum_{i=0}^{N-1} \left(y_{1,i} - y_{2,i} \right)^2 $$

Imports

import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import convolve

Initial Problem

We want to retreive the horizontal shift between $y1$ and $y2$ in order to find the best overlap between the two curves.

We will call this shift, the offset $o$.

def shift(f, x, shift):
    return f(x-shift)

def f(x):
    return x*3- x**2
    #return np.sin(x*np.pi/20)
    #return np.exp(x*np.pi/20)*3 

o0 = 20
x = np.arange(0,100,1)
y1 = f(x)
y2 = shift(f, x, o0)

fig = plt.figure(figsize=(4,4))
plt.plot(x, y1, label="y1")
plt.plot(x, y2, label="y2")
plt.title("Initial problem")
plt.legend()
plt.show()

Convolution

c = np.convolve(y1, y2, "full")

plt.plot(c)
plt.show()

print("Convoluton argmax:", c.argmax())
print("Convoluton argmin:", c.argmin())

Convoluton argmax: 167
Convoluton argmin: 2

Conclusion: We see that the convolution doesn't yield the right answer.

Swiping curves

Let's now write a function overlap1 that will compute $d$ for all the possible horizontal translation of $y2$ while keeping $y1$ fixed.

def overlap1(y1, y2):
    """
    overlap computes the mean quadratic difference between y1 and y2
    at several overlapping positions.
    we adjust the overlaps so that there is always the same amount of points
    that are used in the averages.
    A better way would be to compute an horizontal distance as with Lebesgue
    integral. However, it is perhaps impossible numerically...
    """
    x = y1 if len(y1) >= len(y2) else y2 # long
    y = y2 if len(y1) >= len(y2) else y1 # short
    # slide short over long
    m = len(x)
    n = len(y)
    # compute overlaps
    res = [np.sum((x[:i] - y[-i:])**2) for i in range(1, n)]
    res += [np.sum((x[i:n+i] - y)**2) for i in range(0, m-n+1)]
    res += [np.sum((x[m-n+i:] - y[:n-i])**2) for i in range(1, n)]
    return np.array(res)

y1n = y1/np.max(y1) # it is unecessary to normalize here actually.
y2n = y2/np.max(y2)
# we can play and select a piece of y2
imin = 0
imax = len(y2)
ys = y2[imin:imax]
n = len(ys)
# compute the overlap for plotting
op = overlap1(y1n,y2n)

# first plot the initial graph 
# and the overlap mean quadratic differences.
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1.set_title("Intial curves")
ax1.plot(x, y1, label="y1")
ax1.plot(x, y2, label="y2")
plt.legend()

ax2 = fig.add_subplot(1,2,2)
ax2.set_title("Overlap quadratic differences")
ax2.plot(op)

plt.show()

print("Overlap argmax around i=25", op[:50].argmax())
print("Overlap argmin", op.argmin())
print("Overlap argmax", op.argmax())
print("Original offset:", o0)
print("n - argmin - 1 =", n - op.argmin() - 1 )

Overlap argmax around i=25 27
Overlap argmin 79
Overlap argmax 154
Original offset: 20
n - argmin - 1 = 20

Observation: Interestingly, it seems that our naive approach led to a result. However, the overlap function shows a shape that could lead to several local minima. Is it out of luck that we managed to get the good response ?

Let's try on two other functions and let's use another algorithm.

def f2(x):
    return np.sin(x*np.pi/10)

o1 = -10
y3 = f2(x)
y4 = shift(f2, x, o1)

n = len(ys)
# compute the overlap for plotting
op = overlap1(y3,y4)

# first plot the initial graph 
# and the overlap mean quadratic differences.
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1.set_title("Intial curves")
ax1.plot(x, y3, label="y1") # we keep the old names to conserve the same comparison order
ax1.plot(x, y4, label="y2")
plt.legend()

ax2 = fig.add_subplot(1,2,2)
ax2.set_title("Overlap quadratic differences")
ax2.plot(op)

plt.show()

print("Overlap argmax around i=25", op[:50].argmax())
print("Overlap argmin", op.argmin())
print("Overlap argmax", op.argmax())
print("Original offset:", o1)
print("Overlap in 0:", op[0], "compared to min overlap", op.min())
print("n - argmin - 1 =", n - op.argmin() - 1 )

Overlap argmax around i=25 39
Overlap argmin 109
Overlap argmax 99
Original offset: -10
Overlap in 0: 0.09549150281253019 compared to min overlap 0.0
n - argmin - 1 = -10

def f3(x):
    return np.ones_like(x)

o2 = 10
y5 = f3(x)
y6 = shift(f3, x, o2)

n = len(ys)
# compute the overlap for plotting
op = overlap1(y5,y6)

# first plot the initial graph 
# and the overlap mean quadratic differences.
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1.set_title("Intial curves")
ax1.plot(x, y5, label="y1") # we keep the old names to conserve the same comparison order
ax1.plot(x, y6, label="y2")
plt.legend()

ax2 = fig.add_subplot(1,2,2)
ax2.set_title("Overlap quadratic differences")
ax2.plot(op)

plt.show()

print("Overlap argmax around i=25", op[:50].argmax())
print("Overlap argmin", op.argmin())
print("Overlap argmax", op.argmax())
print("Original offset:", o2)
print("Overlap in 0:", op[0], "compared to min overlap", op.min())
print("n - argmin - 1 =", n - op.argmin() - 1 )

Overlap argmax around i=25 0
Overlap argmin 0
Overlap argmax 0
Original offset: 10
Overlap in 0: 0 compared to min overlap 0
n - argmin - 1 = 99

Observation: we see that our algotithm seems to work well on functions that show some variation but fail on a flat line. To be honest, the flat line does't show any offset and the answer should have been 0. Here, it means that any position give the same distance. However, it seems that the first absolute minima alway provides the right answer. Strangeley, numpy.argmin is supposed to return the first argmin found.

Conclusion: the algorithm works for pieces of the same lengths and the special case of flat lines has to be trated seperately.

Now let's change the algorithm to improve this first work.

Final Solution

Here, we reuse the work done previously, but we change the distance from $d$ to $d_{m}$. It graphically improves the interpretation of the shape of the overlap funtion.

def overlap(y1, y2):
    """
    overlap computes the mean quadratic difference between y1 and y2
    at several overlapping positions.
    we adjust the overlaps so that there is always the same amount of points
    that are used in the averages.
    A better way would be to compute an horizontal distance as with Lebesgue
    integral. However, it is perhaps impossible numerically...
    """
    x = y1 if len(y1) >= len(y2) else y2 # long
    y = y2 if len(y1) >= len(y2) else y1 # short
    # slide short over long
    m = len(x)
    n = len(y)
    # compute overlaps
    res = [np.mean((x[:i] - y[-i:])**2) for i in range(1, n)]
    res += [np.mean((x[i:n+i] - y)**2) for i in range(0, m-n+1)]
    res += [np.mean((x[m-n+i:] - y[:n-i])**2) for i in range(1, n)]
    return np.array(res)

def get_offset(y1,y2):
    """
    this funcions returns the horzontal shift between the array y1 and y2.
    This shift is taken as the minimal average quadratic difference between
    overlapping sections of y1 and y2.
    """
    n = len(y2) if len(y2) >= len(y1) else len(y1)
    op = overlap(y1,y2)
    am = np.argmin(op)
    # if the line is flat
    if op[am] == op[0]:
        return 0
    # in the other cases
    else:
        return n - am - 1

y1n = y1/np.max(y1)
y2n = y2/np.max(y2)
# it is unecessary to normalize actually.
step = 33
# we can play and select a piece of y2
imin = 0
imax = len(y2)
ys = y2[imin:imax]
# compute the overlap for plotting
op = overlap(y1n,y2n)
# compute offset to check answer
o = get_offset(y1,y2)

# first plot the initial graph 
# and the overlap mean quadratic differences.
fig = plt.figure(figsize=(12,4))
ax1 = fig.add_subplot(1,2,1)
ax1.set_title("Intial curves")
ax1.plot(x, y1, label="y1")
ax1.plot(x, y2, label="y2")
plt.legend()

ax2 = fig.add_subplot(1,2,2)
ax2.set_title("Overlap mean quadratic differences")
ax2.plot(op)

plt.show()

# plot results
plt.plot(x, y1, label="y1", linewidth=2, linestyle="dashed")
plt.plot(x[imin:imax]-o, ys, label="y2 + offset", linewidth=1)
plt.legend()
plt.show()

# print offset
print("Original offset", o0)
print("Computed offset:", o)

Original offset 20
Computed offset: 20

Conclusion: we managed to come up with an algorith to find the best overlap between two curves given a quadratic average distance. The fact of averaging renormalizes the contribution of each overlapping interval and provides a clearer overlap graph to interpret.